�n���𑪂�@����2�@�n�`�}�@Topographic maps�@�@2024�N8��31��version
1 �n�`�}����
1.1 �ܓx�ƌo�x
1.2 �O�p���ʂƎO�p�_
2 ���y�̊�{�}
2.1�ɔ\���h�u����{���C�`�n�S�}�v
2.2�n�`�}�쐬�̗��j
3 ���ʋZ�p�̐i�W
4 ���ʂ̉��p
2000�N�L��R(��������)�̕���
5 ���K�F�n�`�}��ǂށ@
6 ���K�F���ʂ̊�{
6.1�O�p���̕��K�@�@
6.2���ʂ̌���
7���K�F�q��ʐ^�̗��p(���̎�)
�⑫�F�o�x�̗��j
�t�^�F�������當�ɂ⓮��̏Љ�
------------------------
�n�`�}�̓������ŎR��J�̌`��m��C�ܓx�ƌo�x�ŏꏊ��m��
�l�H�q����V�̗̂��p�ő��ʋZ�p�����������Ă���
���ʂő�n�̕ω���m�邱�Ƃ��ł���
------------------------
���K�̌����������邽�߁C�{�����̖₢���܂Ƃ߂ċL���B
��1�@�n�`�}�̓����������ݍ����Ă���Ƃ���͒n�`�I�ɂǂ�ȂƂ��납�B�\�z�����n���ЊQ�͉����B
(���1�܂Ƃ߂̉�)�@
��2�@���R�s�����͖k��35.4�x�C���o136.9�x�C�D�y�s�͖k��43.1�x�C���o141.3�x�ł���B������̑��z�̓쒆(�^��ɗ��邱��)�ɂ��āC�쒆�����͂ǂ̂��炢�Ⴄ���H
(���1�܂Ƃ߂̉��ɋL��)
��3�@����̍ŏ㕔�܂ł̊p�x���R�O�x�C���̖̍����܂�20m�������B���̖̍��������߂�B�������C�p�x�����߂��Ƃ�(�l)�̖ڂ̍����͂P.5m�ł���B
(���2�܂Ƃ߂̉�)�@
=========================
1�@�n�`�}����
1.1 �n�`�}�̊�{���F�������C�ܓx�C�o�x
������
�������͓�����������łނ����́B�R�ɂȂ��Ă���C�J�ɂȂ��Ă���Ȃǂ�ǂ݂Ƃ邱�Ƃ��ł���B���̐}�́C���̓I�ȉ摜�ɓ��������d�˂����́B
�n�`�Ɠ������̊W(�E�B�L�y�f�B�A���)
https://upload.wikimedia.org/wikipedia/commons/4/4c/Topographic-Relief-perspective-sample.jpg
�������̕��������Ƃ���͋}�C�������̕����L���Ƃ���͂��₩�Ȃ��Ƃ��킩��B
-----------------
��1
�n�`�}�̓����������ݍ����Ă���Ƃ���͒n�`�I�ɂǂ�ȂƂ��납�B�\�z�����n���ЊQ�͉����B
(���1�܂Ƃ߂̉�)
-------------------
�ܓx�ƌo�x
�ܓx�F�ԓ�����Ƃ��ē�k�ւ��ꂼ���܁C�k�܂Ƃ���90�x�܂ł�\���B
�o�x�F�p���̃O���j�b�W�V����Օt�߂�ʂ�q�ߐ�(��������G�ԓ��ɒ�������n����̓�k�̐�)����ɓ����ւ��ꂼ��o�C���o�Ƃ��āC180�x�܂ł�\���B
�ܓx�o�x(�E�B�L�y�f�B�A���)
���݂́C�l�H�q������̓d�g�𗘗p���ėe�ՂɈܓx�ƌo�x��m�邱�Ƃ��ł���B�Ƃ��낪�ق�̐��\�N�O�܂ŁC��̓_�̈ܓx�o�x�����߂�ɂ͓V�̂̊ϑ�����b�ɂ��āC���܂��܂ȕ���s���Ȃǂ��Ď��Ԃ����������B
�ܓx�́C�k�ɐ��ƒn�����Ƃ̊p�x�ŋ��߂���B�ܓx�̈Ⴂ�́C�������̑��z�̓쒆�p�x�̍��ƂȂ�B(�쒆�F ���z���^��ɂ��邱��)
�o�x�͒n�������360�x�C�n����1��](�P��)��24���ԁC������1���Ԃ�360��24��15�x�ƂȂ�B���{�̕W�����q�ߐ��͓��o135�x�Ƃ��Ă���̂Ő��E�W����(�O���j�b�W�V����ł̎���)��135��15��9���Ԃ̍�������B���{�����ł����������邪�C���o135�x�̎����œ��ꂵ�Ă���B�����œ��قǓ��̏o�̎����������Ȃ�B
----------------
��2
���R�s�����͖k��35.4�x�C���o136.9�x�C�D�y�s�͖k��43.1�x�C���o141.3�x�ł���B
������̑��z�̓쒆(�^��ɗ��邱��)�ɂ��āC�쒆�����͂ǂ̂��炢�Ⴄ���H
(���1�܂Ƃ߂̉��ɋL��)
-----------------
1.2�O�p���ʂƎO�p�_
���R�ȏꏊ�ɂ���Q�_�Ԃ̋����𐳊m�ɑ���B�����P�_�������ĎO�p�`�����C�O�p�`�̓��p�𑪂�B�v�Z�ŋ��߂���1�_�̈ʒu�����߂�B����ɓ_�𑝂₵�ĎO�p�`�̖Ԃ����C�e�_�̈ʒu�����߂Ă����B
���y�n���@�̐����C�}�Q��
https://www.gsi.go.jp/sokuchikijun/sankaku-survey.html
�O�p�_
�O�p���ʂ��s���ہC�o�x�E�ܓx�E�W���̊�ɂȂ�_�B���̎ʐ^�Q��(�E�B�L�y�f�B�A���)
https://upload.wikimedia.org/wikipedia/commons/2/25/1_tou_sankakuen.jpg
�E�O�p���ʂƂ́C�n��Ŏ��ۂɑ�������{�̐�����b�Ɏ��X�ɎO�p�`�̓��p�𑪒肷�邱�ƂŎO�p�_�̈ʒu�����肵�Ă����B
�E�O�p�_�́C�n�}�쐬�C�e�푪�ʁC�n�k��̕ϓ����ς���Ȃǂŗ��p�����B
�ŋ߂̎O�p�_����
�E�l�H�q�����g���Ĉʒu�����߂邱�Ƃ��ł���BGNSS (Global Navigation Satellite Systems) ���ʂƂ����B
�E���݁C�O�p�_�̑��ʂł͂��̕��@��p���邱�Ƃ������B�ق��̊�������Ȃ��Ă��ʒu�����߂���B
�O�p���ʂ���O�ӑ��ʂ�
�E�O�p�`�̌`�Ƒ傫�������肷��ɂ́C�O�p�`�̎O�ӂ̒����𑪒肵�Ă��悢�B�����̑��ʂ͏]�������̘J�͂������������C�ŋ߂͌��g���g���ėe�Ղɑ���ł���悤�ɂȂ����B
�E�����͓�_�Ԃ������������鎞�Ԃ𑪒肵�Ă���Ɍ����x���������̔������Z�o����B���g�����V�����������ˋ��Ŕ��˂��Ă���̂��Ƃ炦��B
�E�����x��30���L��/�b��1�p�̐��x�ŋ��������߂�ɂ͎��ԍ���3�~10-11�b�܂ő��肵�Ȃ��Ă͂Ȃ�Ȃ��B���݂͂܂�����Ȃ̂Ō���ϒ����Ĕg�ɂ��Ă��̐��ŋ��߂Ă���B
---------------------
1�̂܂Ƃ�
�n�`�}�ɂ͓y�n�̊�b������C���R�̂悤��(�R�̌`�Ȃ�)��������ǂ݂Ƃ��B�����̎{�݂͋L���ł��߂���Ă���B�n�`�}�͍ЊQ�\����J���̊�b�Ƃ��ė��p�����B
��1�@��
�}�ȌX�B���ɒ��ӂ���B
��2�̉�
�o�x�̍���141.3-136.9=4.4�x�B15�x��1���Ԃ�����4.4��15=0.29���ԁC�܂�17.6���Ⴄ�B���Ȃ݂ɓ쒆���̑��z�̊p�x�́C�ܓx�̍���43.1-35.4=7.7�x�Ⴄ�B
=======================
2 ���y�̊�{�}�@�n�`�}
���̊�{��m�邽�߂ɐ��m�Ȓn�}���K�v�ƂȂ�B�]�ˎ���Ɉɔ\���h�Ƃ��̒�q�����{�S�y�̒n�}�����������B�����ɂȂ�C���{�̋ߑ㉻�̒��Œn�}(�n�`�})����������Ă���B��O�̎Q�d�{�����n���ʕ�(�肭��������傤��)���猻�݂̍��y�n���@(�����ǂ����)�܂ŗ��j������B
2.1�ɔ\���h�u����{���C�`�n�S�}�v
�]�ˎ���Ɉɔ\���h(���̂����������@1745-1818)���C1800�N����1816�N�܂ŁC17�N�����ē��{�S���𑪗ʂ��āu����{���C�`�n�S�}(�����ɂق��悿����)�v�������������B
���ʂ̗l�q���t�^�̓���Œm�邱�Ƃ��ł���B
�ɔ\���h�̒n�}�̈ꕔ�@(��������)�@(�E�B�L�y�f�B�A���)
--------------
2.2�n�`�}�쐬�̗��j
�����ɂȂ�ƍ��̍������Ȃ����ƂƂ��Ēn�`�}�쐬�����肳�ꂽ�B
��O�͎Q�d�{�����n�`�}���NJ�(����)����B���݂Ɏ���܂ł̗��j�͎��̒ʂ�B
1869:
�������ːВn�}�|�C���̌�C�����ȁC�H���ȁC�����ȁC�����ȓ��X�ɏ���
1874:
�����Ȓn�����C
1875:
��O�p���ʎ���(�ꓙ�O�p����)���J�n
1888:
�Q�d�{�����n���ʕ�
1892:
���{�o�x�ܓx���_��ݒu(�������z)
���c�傩��]�ޗ��n���ʕ�(���������B�e�C�E�B�L�y�f�B�A���)
https://upload.wikimedia.org/wikipedia/commons/7/7e/IJA_General_Staff_HQ.jpg
���{�o�ܓx���_(�`�旧���y���j��)
https://www.minato-rekishi.com/museum/2009/10/88.html
1915:
�ꓙ�O�p���ʊ���
1924:
�S��5������1�n�`�}����
1945:
�����Ȓn��������
1948:
���ݏȒn��������
1950:
2��5�番��1�n�`�}�쐬�J�n
1960:
���ݏȍ��y�n���@�C�y�n���p�����C�V���E�n���C�E�d�͊ϑ��ȂǑ���
1983:
2��5�番��1�n�`�}�S����������
2001:
���y��ʏȍ��y�n���@�C�Ȍ�}���ɒn�}���̓d�q�����i��
------------------------------------
3 ���n�Z�p�̕ϑJ
���̐߂̂��Ȃ�̕����́C����(2003)���Q�l�ɂ����B
���ʋZ�p�̕ϑJ(����p��C2003�C���ʋZ�p�̕ϑJ�D�d�w���C123�C813-816�D)
(a)
���h�̈ܓx�ϑ��Ǝq�ߐ��ʒ��̊ϑ�
�E1800�N �Ɉɔ\���h�� �u���{�}(���{�S�̂��\���ꂽ�})�v���ɒ���B
���j�V�ɂ��p�x(����)����ƁC�������ɂ�鋗�������,�����g���Ĉܓx��
��u�V���v�̕��@�������ʒu�m�F���s���B
(b) �o�x���ʂ̊J�n
�E1871(��4)�N �ɃE���W�I�X�g�b�N�ƒ�������ԑ嗤�ւ̊C��P�[�u�����~�݂���,���{�͍��ۓd�M�ԂɌ���C�A�����J�l�Ȋw�҂ɂ���Čo�x���ʂ�����7�N�Ɏ��{�B
���������̎��v��d�M�ō��킹��,���ꐯ�̎q�ߐ��ʉ߂����ꂼ��ő��肵,���̑��莞�ԍ�����o�x����B
(c)
�O�p�_�̐�����5������1�n�`�}
�E1884(����17)�N�C���߂ăC�M ���X�O���j�b�W(���E�̌��_)�ƌ��ꂽ������ �u���o�ܓx���_�v���a����,�O�p���ʂ̌v�Z���q������B���̌��_�����ƂɈꓙ�O�p���ʂ��i�߂��,�吳2(1913)�N�Ɋ��� �����B
�E1924(�� ��13)�N�C3��9��_�̎O�p�_�̌o�ܓx�����ƂɁC�u��{�}(����5������1�n�`�})�v�������B
(d) �o�܋V����g�[�^���X�e�[�V������(���y�������Ƃ�������ʂ̐i�W�̒���)
�E1951�N�̍��y�����@�Œn�Ђ� �炩�ɂ����b�����Ƃ��Ďl���O�p���ʎ��Ƃ��s����B�l���O�p���ʂ̑��ʋ@��́C�������炵�炭�͌o�܋V���g�p���ꂽ�B
�E�d�q�@�� �̊J���ɔ����p�x��30�b����1�b�ǂ݂ƂȂ�C�����,���g(���[�U)��p���������ϑ��������ɉ\�Ƃ����g�[�^���X�e�[�V ����(TS)�𗘗p�B
�E�g�[�^���X�e�[�V�����́C�c��ȃf�[�^��Z���Ԃň����y�؎��Ƃ̂��߂̌������ʂŗ��p�����B
���w�I���ʊ�@�͓��{�ł͌o�܋V�Ƃ��Ă������C���̂����o�[�j���ڐ���Ŋp�x���͂�����̂��u�g�����V�b�g�v�C���������������x�Ղ̐������}�C�N�����[�^�[�œǂݎ��C���邢�̓f�W�^���f�B�X�v���[�\���̂��̂��u�Z�I�h���C�g�v�Ƌ�ʂ��Ă���B
�g�����V�b�g�@�E�B�L�y�f�B�A���
https://upload.wikimedia.org/wikipedia/commons/6/6b/Kern_Theodolit_DKM2-A.jpg
�Z�I�h���C�g�@�E�B�L�y�f�B�A���
https://upload.wikimedia.org/wikipedia/commons/4/4b/Taqu%C3%ADmetro_Sokkisha_TM20H_%282%29.jpg
(e) ���E���n�n�̓���
�E�l�H�q���̊ϑ����琸���Ȓn���̌`��������悤�ɂȂ�C�������Ɍ��߂�ꂽ���{���n�n�őz�肵���n���̑ȉ~�̂̌`�E�傫���₻�̒��S�ʒu�������قȂ邱�Ƃ����炩�ɂȂ�B
�E2002�N4���C���ʖ@�̉����œ��{�̈ʒu�𐢊E���n�n�ɂ����悤�ύX�����B
�E���̍ہC�O�p�_�Ȃǂ̍��Ɗ�_�̈ʒu�́CVLBI (Very Long Baseline Interferometry ��������d�g���v)��GPS�Ȃǂ̑��ʃf�[�^�����ƂɏC�����ꂽ�B
�⑫�F�n���ȉ~��
(���̍��͓���z��Y(1994)�n���̌`�Ƒ傫���D�V�Œn�w����u���u�n�����͂���v�C1-49�D���Q�l�ɂ���)
�E16���I�ɂ͒n�������`�ł��邱�Ƃ͒萫�I�ɂ͂킩�������C���̑傫�����ǂ̂��炢���C����Z�p�̐i���ƂƂ��ɉ��������Ԃ����肪�s��ꂽ�B
�E17���I�㔼�ɂ͒n�����͂����Ċ��S�ȋ��Ȃ̂��^�₪�������悤�ɂȂ����B�t�����X�Ȋw�A�J�f�~�[���t�����X�̃M�A�i�ɉ����������C�k��5�x�ŐU�q���v�𐳂����ۂɂ͖k��49�x�̃p���Ő��������킹���U��q���v�̐U�q��Z�����Ȃ���Ȃ�Ȃ����Ƃ��킩�����B�n�����ԓ��t�߂łӂ����ł���Ƃ���ΐ��������B���̐��ʂ�1684�N�Ɍ��\���ꂽ�B
�E18���I�C�n���̐ԓ����a�Ƌɔ��a���ǂ̂��炢�Ⴄ���C�Ε�����(�ԓ����a�[�ɔ��a)/�ԓ����a�����߂邱�Ƃ��t�����X�𒆐S�ɂ��đ�����ꂽ�B19���I�ɂ͎O�p���ʂ̎O�p�Ԃ��Ђ낪��C���̌��ʁC���낢��̒n���ȉ~�̂���Ă��ꂽ�B
�E20���I�㔼�ɂ͐l�H�q���̌��ʂ��Ƃ肢��C���E���n�n�̍��ۑȉ~�̂��g���悤�ɂȂ����B�����GPS���p�̑O��ƂȂ�B
�n���ȉ~��(�E�B�L�y�f�B�A���)
(f)
�d�q��_
�E�O�p�_�ɑ���d�q��_��S���ɖ�1,200�_(��25km��1�_)�z �u ���āC24���ԏ펞�ϑ�����悤�ɂȂ�B
�E�d�q��_�Ƃ́C�l�H�q���̓d�g���Đ��m�ȑ��ʂ��s�����߂̊�_�B
�E�d�q��_���m�̑��ΓI�Ȉʒu�W�𗘗p���āC�n�k�ϓ��̊Ď��ɗ��p�����B�Ⴆ�C�����ϓ��ʂ��瓌���{�Ɛ����{�ňقȂ邱�ƂȂǂ����ĂƂȂ�B
(g) VLBI����
�E���\�����N�̉F���̂��Ȃ��ɂ���d�g��(����:�N�G�[�T)������o�����d�g��n�\2�n�_�œ����Ɋϑ���,���̓��B���Ԃ̍������M�A���e�i�Ԃ̑��Έʒu�W(����x�N �g��)�������x�Ō��肷��B
�E���{�ƃn���C�̊�
��VLBI�Ŋϑ���������,1�N�Ԃɖ�6cm���n���C���߂Â��Ă��邪�킩��B
=================
4 ���ʂ̉��p���@2000�N�L��R(��������)�̕���
�L��R�́C�k�C���L��S�s�˒��C�k�C���̓쐼���C����̓�Ɉʒu����B
�L��ΎR�́C�قڒ���I�ɂ��̂悤�ȉΎR����������B
1663�N�C����⎿�y�Ε��o
1769�N�C���a�M�_�C���L��`��
1822�N�C�����M�_�C
1853�N�C��L��`��
1910�N�C�����V�R�`��
1944-45�N�C���a�V�R�`��
1977-78�N�C�y�Ε�����}�O�}�����C��L�엲�N�C���L�쒾�~
2000�N�C�L�앬��
�L��R�S�i(�E�B�L�y�f�B�A���)
https://upload.wikimedia.org/wikipedia/commons/2/20/%E6%9C%89%E7%8F%A0%E5%B1%B1.jpg
���Ό��߂��Ŕp�ЂƂȂ����R�[(�E�B�L�y�f�B�A���)
https://upload.wikimedia.org/wikipedia/commons/8/8a/Mount_Usu.jpg
���N���Ēn���ꂵ�����H(�E�B�L�y�f�B�A���)
�@https://upload.wikimedia.org/wikipedia/commons/a/a0/UsuZan2007Ryuki.JPG
���ʎ���
���Ύ��ɂ́C���̒n��͗�������֎~�̂��߁C���S�Ȏ��͂��畬�Βn����ɖڕW���߂đ��ʂ��s�����B�Ⴆ�Ό����̉����̊p�Ȃǂ�ڕW�Ƃ����B���ʖ@�̌�����2��������ڕW�ւ̕��ʂ�p�x�𑪂�C�ڕW���̓������Ƃ炦���B����I�Ɋϑ����āC�ڕW�_�����N���邢��)���Ƃ��킩��B���̂����ɂ��̓����͎~�܂�C�ΎR�̊����͎��܂�Ɣ��f�ł����B
���ʌ���(�n��������2001�̈ꕔ���p)
���@http://y95480.g1.xrea.com/nue_mineral_5_gsj2001fig11.pdf
���N(Uplift)��7��22�����Ŏ~�܂�C�ΎR�̊��������܂�Ɣ��f�ł���������i�߂�B
-------------------
�L��R2000�N���ł͐l�I��Q�[��
�l���ł̕��ɂ�������炸�C���ɂ��]���҂�1�l�����Ȃ������B�l�I��Q�[�������̃|�C���g�͎��̒ʂ�B
�E�����X�N�̍��܂��I�m�ɋ��L�ł����B
�E���ׂĂ̏Z���������E���w���������C�\�莞�ԓ��ɔ����Ȃ��Ƃ����B
(�{�L�r�F�@�L��R�l�I��Q�[���̋��P�@�n���E�n�}�����C2017�N�x2�w��2��)
�Q�l�F���a�V�R�̑���
�O��̒n�w�j�ŁC�L��R�̂ӂ��Ƃ�1943�N�ɏ��a�V�R���o�����C���̐������L�^�����O�����v�����Љ���B�t�^�̓���ŁC�O�����v���̊����̃j���[�X�����邱�Ƃ��ł���B
==================
5 ���K�F�n�`�}��ǂ�
���y�n���@�̒n�`�}
���y�n���@�̒n�`�}�͈�����ꂽ���̂��s�̂���Ă���B
���݂́C�f�W�^�������i�݁C�E�F�u�ŔC�ӂ̏ꏊ�̒n�`�}�����邱�Ƃ��ł���B
https://maps.gsi.go.jp/#5/36.102376/140.097656/&base=std&ls=std&disp=1&vs=c1j0h0k0l0u0t0z0r0s0m0f1
�g�����F
�E�C�ӂ̏ꏊ�Ɉړ�����B
�E+/-�Œn�}�̑傫����ς���B
�E���j���[�o�[�̃c�[���𗘗p����ƒn�`�f�ʍ쐬��3D�\�����ł��C������ʐς̌v�����ł���B
�n�`�}�̒n�}�L��
�n�}�L���ꗗ�͎��̒ʂ�(Mapion���)�@(���y�n���@�n�`�}�ȊO�Ŏg���L�����܂�)
https://help.mapion.co.jp/map/mark/mapnote.html#map
https://help.mapion.co.jp/map/mark/notation.html
��w�t�߂Œn�`�}�ɐ����Ă�����e�����Ă݂�B
���É��o�ϑ�w�t�߂̒n�`�}�͎��̒ʂ�B
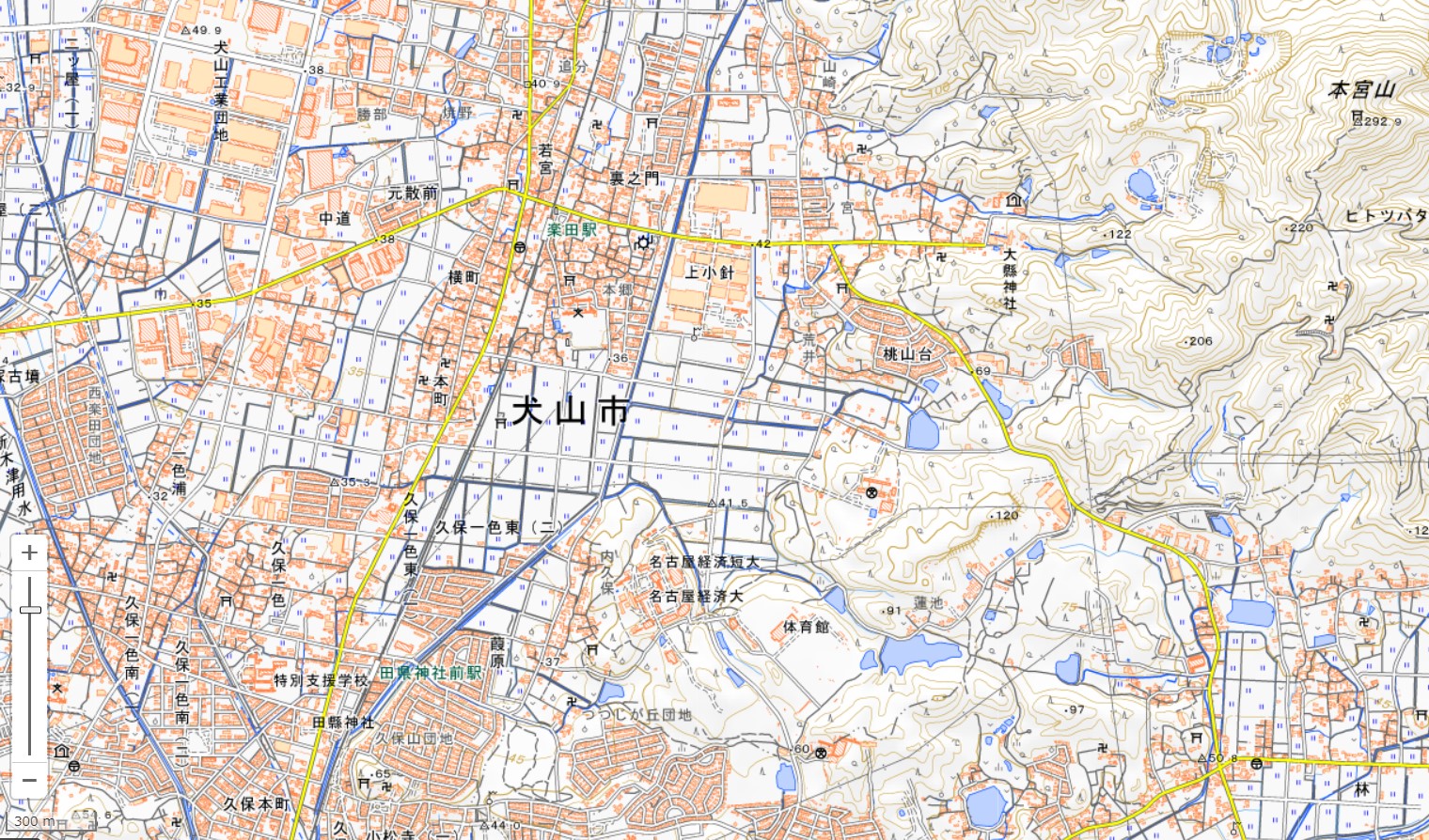
�ȉ��̂��Ƃ��m�F���Ă݂�B
�E���É��o�ϑ�w�̖k(��)�̕��ɓc��ځu�L���F�����v���L�����Ă���B
�E��w�̓쐼(����)�ɐ_�Ђ⎛������B��(��)�ɏZ��L�����Ă���̂��킩��B
�E�k��(�E��)�ɖ{�{�R������B���̎���͓����������ݍ����R�ł��邱�Ƃ�ǂ݂Ƃ��B
�E�{�{�R�̎R���ɎO�p�_�u���v������C���̍���(�W��)��292.9���ł���B
==================
6 ���K�F���ʂ̊�{
�O�p���̕��K
�n�}�����̂Ɋ�ƂȂ�_����O�p�`�Ŋe�_�̈ʒu�����Ɍ��߂Ă����B���̂Ƃ��O�p�����g���B
�ȉ��͎O�p����Y�ꂽ�l�̂��߂ɗp�ӁB�g�ɂ��Ă���l�͂Ƃ��B
���p�O�p�`���l����B
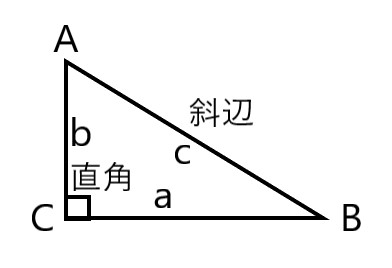
�O�p���͎��̂悤�ɒ�`�����B
�T�C��B�@�@ �Fsin B = b �� c (���邢��b/c)
�R�T�C��B �Fcos B = a �� c (���邢��a/c)
�^���W�F���gB�Ftan B = b �� a (���邢��b/a)
��\�I�ȗ�
C�̊p�x�����p(90�x)�̎O�p�`�Ƃ���ƁC
�EB�̊p�x��30�x�CA�̊p�x��60�x�ł́C
a=���[�g3(= 1.73),
b=1, c=2
���ꂩ��sin 30 = 1��2 = 0.5, cos 30 = 1.73 ��2 = 0.87, tan 30 = 1��1.73 = 0.58
�EA�̊p�x��B�̊p�x���Ƃ���45�x�ł́C
a=1, b=1, c=���[�g2(= 1.41)
���ꂩ��sin 45 = 1��1.41 = 0.71, cos 45 = 1��1.41 = 0.71, tan 45
= 1��1 = 1
�C�ӂ̎O�p���̒l�́C�\���邢�̓X�}�z�ŋ��߂�B���͕\�ɂȂ������́B
�O�p���\(PUKIWIKI)
--------------------
���
���̐}���Q�Ƃ��āC�݂��牫�̑D�܂ł̋��������߂邱�Ƃ��s���B
https://upload.wikimedia.org/wikipedia/commons/8/80/Distance_by_triangulation.svg
(�}�̓E�B�L�y�f�B�A���)
I�̒�����ℓ�Ƃ���Ȃ�
ℓ = d/tan �� + d/tan ��
�䂦��
d
= ℓ/(1/tan �� + 1/tan ��)
----------------------
��3�@����̍ŏ㕔�܂ł̊p�x���R�O�x�C���̖̍����܂�20m�������B���̖̍��������߂�B
�������C�p�x�����߂��Ƃ�(�l)�̖ڂ̍����͂P.5m�ł���B
���6�܂Ƃ߂̉��ɋL���B
-----------------------------
6�̂܂Ƃ�
�n�`�}����鑪�ʂ͎O�p���ʂ���{�ł���B���̂��߂ɂ͎O�p���̒m�����K�v�ƂȂ�B���ʂ��s�����ƂʼnΎR�̎R�̕ω��̊ϑ��ȂǁC���u�Œn�`�̕ω���m�邱�Ƃ��ł���B
��3
��
20m�@���@tan
30 =20 x 0.58 = 11.6 m, ����ɖڂ̍���1.5 m�������C13.1 m
=========================
7 ���K�F�ʐ^���ǁ@(Aerial photo judgment)
�ꏊ�����炵�ĎB�����ʐ^�𗼖ڂŌ���ƎR��J�Ȃǂ̌`��������B���̎����邢�͗��̎��ƌ����B���f�w��n����n�`�Ȃǂ�ǂ݂Ƃ�ɗL���B�����ŗ��̎���̌�����v
�E���̎�(���̎�)�F�n�}�쐬�p�ɎB�e���ꂽ�ʐ^�ׂ̗荇���ʐ^�̉摜�݂̌��ɏd�����镔�����g���ƁC�摜�����̓I�Ɍ����C���̎����͗��̎��ƌ����B
�E�ʐ^���ʁF���̎����邱�Ƃɂ�莋��ɓ������e�����̐����ʒu�W��䍂�����ώ@���C�n�}�����Ă������ƁB
�E���̎��ɂ�钲���F�n�`�E�n���C�y�n���p�C�A��(�y�n�핢)�C�n���ׂ�E����E�����E�^�����ɌW���ЊQ�n�`���̒����̍ۂ͋ʐ^�̎��̎����K�v�ȋZ�@�ɂȂ�B
--------------------
���̎������݂�
�Ƃ�������̉摜�����Ă��ꂪ��ɂȂ�悤��(�C������)����ƁC���̓I�Ɍ�����B�͂��߂͂Ȃ��Ȃ��ł��Ȃ����C��x������Ƃ��ꂩ��͕ʂ̎ʐ^�ł�������悤�ɂȂ�B
���������܂葱���Ă���ƋC�����������Ȃ�̂Ŗ��������Ȃ��B
��F�|�c���--�V��̏�C���Ɍ�����(������)�s
�e���̂����ŁC���E�̖ڐ��s�C���邢�͌������Č���B
�ȉ��ɂ͂��ꂼ��ɑΉ��ł���悤���������B�����ŎR���ւ���Ō�����ꍇ�C��������̎ʐ^�Ŏ����Ă݂�B
�܂��C�摜�������߂ɂ����������̎����₷���̂ʼn�ʂ̑傫��������B
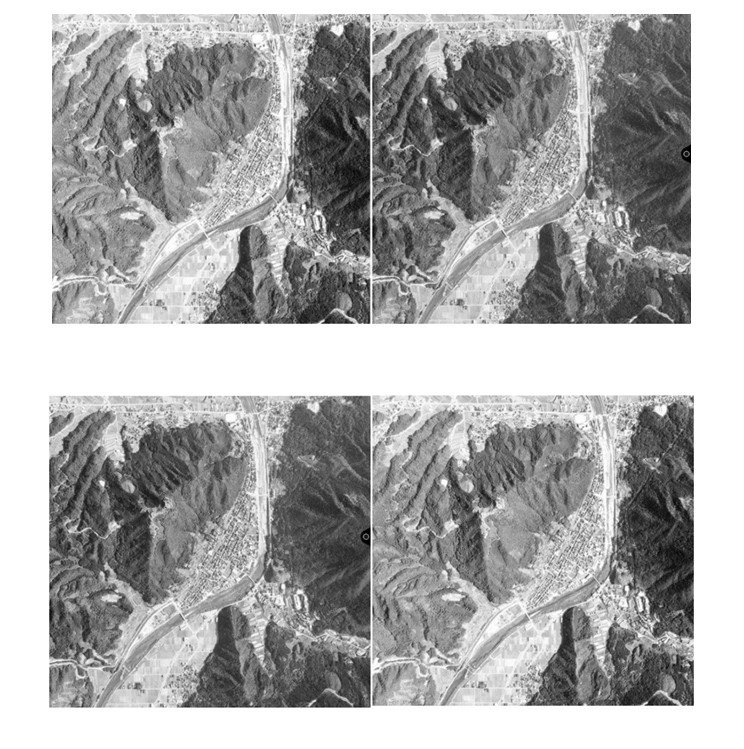
--------------------
���̂ق��̗�
�y�؏��T�[�r�X�@�����ڂ��l�b�g
https://isabou.net/TheFront/disaster/geology/Hypostatize/zittai.asp
���̎��̌����ƃT���v��
---------------------
7�̂܂Ƃ�
�ꏊ�����点�ĎB�e�����ʐ^���g���Ǝ��̎�(���̎�)���ł���B���̂��ƂŒn����n�`�̒����Ɏg���C���f�w��n���ׂ�n�`�̔��ǂ��ł���B
�o�x�̗��j
�������n����̂ǂ��ɂ��邩�́C�ܓx�o�x����m�邱�Ƃ��ł���B�ܓx�͔�r�I�e�Ղɂ킩�邪�C�o�x�����߂邱�Ƃɂ͕ϑJ���������B
���̐߂̎�ȎQ�l�����F
���I�l(�������䂤��)2010�@�o�x�̔����Ƒ�p�鍑�D�O�d��w�o�ʼn�Cpp.261�D
��
�E�G���g�X�e�l�X�́C�V�F�l(�A�X����)�ƃA���L�T���h���A����������Ƃ��Ă���ɕ��s�ɐ��{�̒������������B
https://upload.wikimedia.org/wikipedia/commons/e/e8/Mappa_di_Eratostene.jpg
�G���g�X�e�l�X�̒n�}(19���I�ɕ����������́C�E�B�L�y�f�B�A���)
�E�w���j�Y�����C�q�b�p���R�X(Hipparchos, BC190-BC125)�́C�e�n�_�����肷�邽�߂̍��W�n�Ɍo�ܐ��Ԃ��l����B���H�̊J�n�ƏI�������̍�����o�x�����߂��B
�E�A���L�T���h���A�̃v�g���}�C�I�X�́C���[�}����ɂȂ�C�e�n�̒n����������C���E�e�n8000�����̌o�ܓx���L�����B
�o�x�̊�u�{���q�ߐ��v�́C���E�̍Ő��[�ƍl�����Ă����J�i���A�����́u�K�������v�ߕӂ�ʉ߂���q�ߐ��ł������B
15���I����
�������[���b�p�ł̓v�g���}�C�I�X�̉e���͂������Ă������C15���I�����ɃM���V���ꂩ�烉�e����ɖ|��C���[���b�p�ɂ�����v�g���}�C�I�X�́u�Ĕ����v�ƂȂ�B
���E�̗֊s�́u���m���v�̌��オ�ۑ�ƂȂ�B����͊e�n�̌o�x���s���m�C�܂�o�x����@���ۑ�ł������B
�w�i�́C��q�C����ƂȂ�C��C���ł̈ܓx�o�x�̌���̕K�v�����������B
�Ⴆ�R�����u�X�́C�ܓx�͔�r�I�e�Ղɂ킩��̂ŁC�����ܓx�ɉ�����(�ܐ��ɉ�����)���ֈړ����ăA�����J(�T���T�����@�h����)�ɒB�����B�R�����u�X�́C���������[���b�p�l�ɂ܂��m���Ă��Ȃ����n�Ƃ͂킩�炸�C�A�W�A�ƍl�����B�����̒n�}�ł́C�A�W�A���L���l���Ă��āC�A�W�A�̌o�x�����ۂ������ɍL���Ă�������ł���B���Ȃ킿�C�R�����u�X�́C�X�y�C������吼�m��n���ăA�W�A(�W�p���O)�ɒB����̂�4300km�̍q�C�ł��ނƍl���Ă����B����͎��ۂ̋�����3����1���x�������B
https://upload.wikimedia.org/wikipedia/commons/4/4d/Martellus_world_map.jpg
Martellus�̐��E�n�}(1490)�C�E�B�L�y�f�B�A���
https://upload.wikimedia.org/wikipedia/commons/3/36/Columbus_routes.png
��q�C����̉p�Y
�N���X�g�t�@�[�E�R�����u�X
�W�F�m�o���܂�C�|���g�K���ōq�C�p���w�ԁB�@1492�N8��3���D�o�C72���ڂɍ����̐��C���h�����ɒ����B1493�N�̍q�C�Ńv�G���g���R�ɒ����B1498�N��A�����J�嗤�C1502-1503�N�ɂ͍����̃z���W�����X��j�J���O�A�ɒB����B
-----
�A�����S�E�x�X�v�b�`(�C�^���A�̍q�C��)
1497�N�����A�����J�ɒB���B1499�N��A�����J�ɏ㗤�B
�A�����J�̖��̂̓A�����S�E�x�X�v�b�`�ɂ��ȂށB�R�����u�X�̖��̓R�����r�A�Ƃ��Ďc��B
----
�o�X�R�E�_�E�K�}(�|���g�K���̍q�C��)
1498�N��]����܂��C���h�̃J���J�b�^�ɏ㗤�C�C���h�q�H���J���B
----
�t�F���f�B�i���h�E�}�[�����@
1519�N�����̃}�[�����C�����C���̌�C�����m�ɏo�ăt�B���s���Ɏ���B1521�N4��27���}�[�����͐�Z���ɎE�����B�c������s��1522�N�Z�r���A�̍`�ɒ����B�n��������C�n�����`�����ؖ����ꂽ�B
-----------------------------------------
�n�}�w�̔��B
�Q���n���g�E�N���[�}�[(�h�C�c�C���w�I�n���w�̌���)
1569�N�C�吢�E�n�}�������B�ނ̖��O�����e���ꉻ����ƃ����J�g���C�����Ŕނ��g�����}�@�������J�g�����e�}�@(�k����̊p�x)�Ƃ���B�ɒn�����ԓ��߂��ɂ���ׂđ傫���\������邪�C2�_�����ԕ����̕��ʊp�͐������\�������B�q�C�p�ł͕��ʊp���d�v�������̂ł��̐}�@�����p�����B
�o�x����@�@16���I
��n�_�̌o�x�̍��ق́C�n�����̍��قł���B�����ł���n�_�Ŋ�ƂȂ�o�x�ł̎�����m�邱�Ƃł���B���z�̓쒆�������قȂ�2�_�Ŋϑ����C���̎��ԍ�����o�x�����߂邱�Ƃ��ł���B
�ǂ̂悤�ɂ��Ď�����m�邩�B�����͐U��q���v�ő��肷�邪�C�D���h���Ɛ����������Ȃ��B����܂����v�͂܂��\�����p�����Ă��Ȃ������B
���H�⌎�H�̎��ԍ�������C�ؐ��̉q���̐H���ϑ�����C���Ɛ��Ƃ̈ʒu�W�𗘗p����(�����@)�Ȃǂ���Ă��ꂽ�B
���̂悤�ɗ���Ōo�x�����߂�Z�p�͂���Ȃ�Ɋm���������C�C��ł͒����Ԍ���I�ȕ��@�͌�����Ȃ������B�ˑR�Ƃ��đD�̑��x���狗�����v�Z���Čo�x�𐄒肵�Ă����B
�E�o�x����̌��ܐ���
1567�C�X�y�C�������C��Ōo�x�����肷����@�J�������ܐ���Ƃ����B���l�̂��Ƃ��I�����_�C���F�l�`�A�C�t�����X�C�|���g�K���ł����{�����B
1714�C�p���Ōo�x�@����
�p���Ōo�x����@�̊J�������コ��C�܋�2���|���h���p�ӂ��ꂽ�B���݂̉��l�ł�100-350���|���h���炢�ł���B
�E�@�B���v(�N���m���[�^�[)�̊J��
1735�C�n���\���C�C���O�����h���������J���V�A���܂�̎��v�E�l�C���uH1�v��^�̋@�B���v���o�����B���̌�C���ǂ��������B
1761�C�uH4�v���B
1767�CH4��W���U�q���v�Ƃ̔�r�����B
1770�C����K1�����������B����������邱�ƂŎ��p���ɓ��ݏo���B
�E�����@
���m�������߂邽�߂̗v����3�������B���Ȃ킿�C
�u���m�Ȑ��\�v�C�u�p�����̊ϑ��@��̉��ǁv�C�u���^���_�̊m��v�ł���B�����͈ȉ��̂悤�ɍ������ꂽ�B
���\�́C�t�����X�e�B�[�h��1725�N�Ƀu���^�j�J���\�C1729�N�ɓV���}���킷�B
�@��Ƃ��āC1731�N�Ɏl���V�C1759�N�ɘZ���V���J�������B
���^���_�́C1756�N�ɃQ�b�`���Q���̃}�C�A�[(Tobias Mayer, 1723-62)���̌n������B
�E�����@�̎��p��
1763�@�l���B���E�}�X�P�����u�p���q�C�҃K�C�h�v�킷�B����͍q�C�Ҍ����̊Ȗ��Ȍ����@�̗��p�p�̉�����ł���B
1767�@�V����̈�Ƃ��čq�C�N�ӊ����B����̓O���j�b�W�q�ߐ��ɂ��āC�N�Ԃ�3���Ԃ��Ƃ̌��Ƒ��z��P���ւ̊p�����̑����\�ł���B����ɂ�茎���@�ɗv���鎞�Ԃ��啝�ɒZ�k����B
�E�L���v�e���E�N�b�N�̍q�C
�o�x����@�̎������ے�����̂��C�L���v�e���E�N�b�N�̎O���̍q�C�ł���B�����m�̓��X�̐��m�ȊC�}���쐬�����B���[���b�p�����ɂ�鑾���m�q�C�̐V����̖��J���ƈʒu�Â����Ă���B
�N���m���[�^�[(�E�B�L�y�f�B�A���)
https://upload.wikimedia.org/wikipedia/commons/9/9b/Chronom%C3%A8tre_%C3%A0_suspension.jpg
�ԓ���ɂ͖��m�Ȋ�����邪�C�o�x�͐l�דI�ɐݒ肷��K�v���������B�o�x0�x�̊�ƂȂ�q�ߐ����{���q�ߐ��ł���B�ߋ��ɂ͐��E�e�n�ł��܂��܂Ȗ{���q�ߐ����g�p���Ă����B
1851�N�ɉp���̃O���j�b�W�V����Ɏq�ߊ��ݒu����C������ʂ�q�ߐ����O���j�b�W�q�ߐ��ł���B1884�N�����q�ߐ���c�ŁC�{���q�ߐ�(�o�x0��)�̓O���j�b�W�q�ߐ������ۖ{���q�ߐ��Ƃ��邱�Ƃ��̌����ꂽ�B
19���I�㔼�C�O���j�b�W�q�ߐ�����Ƃ��Čo�x�����߂邱�Ƃ��s��ꂽ�B����͓d�M�P�[�u���Ŏ��ԍ������߂邱�Ƃ��ł���悤�ɂȂ������Ƃ��傫���B���̂悤�ɓd�M�ƓV�̊ϑ��Ōo�x�����߂���@���p����ꂽ�B
20���I�ɂȂ�ƁC�����ʐM�����p������C�D���疳���̎������M���邱�ƂŌo�x�����߂���悤�Ȃ����B
1960�N�ɐl�H�q���M���𗘗p���Đ��E���n�n������C�����1980�N������n���̐��x�ǂ��`(�����ȉ~��)�����炩�ɂȂ�C�S�n���I���n�n�ֈڍs����B1980�N�ȍ~�C���ےn����]�E��n���Ƃɂ���`�����IERS��q�ߐ����g���悤�ɂȂ����B�O���j�b�W�q�ߐ��́C�o�x0�x��IERS��q�ߐ�����102.478m���̈ʒu��ʉ߂��Ă���B
������GPS�q������̓d�g�ňʒu���킩�悤�ɂȂ����B�������̌덷�Ōo�x�����߂邱�Ƃ��ł���BGPS:�O���[�o���E�|�W�V���j���O�E�V�X�e���C�S�n�����ʃV�X�e���ł���B
GPS�q���̋O���A�j���[�V����(�E�B�L�y�f�B�A���)
https://upload.wikimedia.org/wikipedia/commons/9/9c/ConstellationGPS.gif
�D���pGPS��M�@(�E�B�L�y�f�B�A���)
https://upload.wikimedia.org/wikipedia/commons/f/f4/Global-Positioning-System.jpg
�l�H�q����p�������� GNSS (�S���E���ʃV�X�e��)
��Ƃ���2�_�Ԃ̋�����2�_����̖ړI�Ƃ���_�܂ł̊p�x�𑪂��@���C���ʂɎg���Ă����B���ʂ𗘗p���ĊԐړI�ɋ��������߂����ɁC���[�U�[�Œ����ɋ����𑪂邱�Ƃ��ł���悤�ɂȂ葪�ʂ̎�Ԃ��傫���Ȃ����Ȃǂ������C���炭�́C���W(�ܓx�o�x)����ɂ́C���m�̊(�O�p�_)���Q�Ƃ��Ȃ��狁�߂��B
���݂́C�l�H�q����p���Ă��̏ꏊ�̍��W(�ܓx�o�x)�����肵�C���ꂩ��2�_�Ԃ̋�������ʂȂǂ̈ʒu�W�����߂邱�Ƃ����ʂƂȂ��Ă���B�����GNSS(Global Navigation Satellite System: �l�H�q���𗘗p�����S���E���ʃV�X�e��)�Ƃ����B
GNSS�̌���(�v���E�����@�푍��Web�W)
���ʉq����4�@�p���āC�ʒu���(X,Y,Z)���擾����B
�u�����v�Ɓu4�@�̑��ʉq���v�Ƃ̋��������ꂼ��v�Z��4�̋��������߂�B����4�̋������ЂƂɌ����_�𐔊w�I�Ɋ���o���C�����̈ʒu�����߂�B
�y���ʉq���Ǝ����܂ł̋������d�g�̑��x
X �d�g�`�����ԁz
�E�d�g�̑��x��299,792,458m/�b
�E�d�g�`�����ԁF�u���ʉq������o���d�g�v���u���[�U�̎���M�@�v�ɓ͂��܂ł̎���
���ʉq�����瑗�M�����d�g�ɂ́u���M���������v�̏�����Ă���̂ŁC�u���M���������v�Ɓu�����̂Ƃ���ɓd�g���������������v�Ƃ̍��Łu�d�g�`�����ԁv���킩��B
�v�Z���3�̋��������Ύ����̈ʒu������ł��邪�B��M�@�̎��v�ɂ͂킸���Ɂu�덷�v������C3�@�̉q���ł͈ʒu���ɃY����������B���̌덷����邽�߂ɂ����P�@�̏����g���B
https://www.gsi.go.jp/denshi/denshi45009.html
���y�n���@(GNSS��p��������)
��L������͂��̃T�C�g�̍ŏ��̒P�Ƒ��ʁB�������ʂȂǏڂ��������B
VLBI(VLBI:
Very Long Baseline Interferometry ��������d�g���v)
�E�d�g�V���w���甭�W�����Z�p�𑪗ʂɉ��p�B
1.�����ɂ���V�̂����d�g���p���{���A���e�i�Ŏ�M����B
2.�A���e�i�̈ʒu�ɂ���ēV�̂���̋������킸���ɈႤ���߁C�d�g����M���鎞�Ԃ����������Ⴄ(0.02�b�ȉ�)�B
3.���ꂼ��̃A���e�i���d�g����M���������̍�������o���B
4.�����̍��ɓd�g�̑����������C�V�̂̕������l�����ăA���e�i�Ԃ̋��������߂�B
5.���̂悤�Ȃ��Ƃ𑽂��̓V�̂ōs���C�A���e�i�Ԃ̈ʒu�W�����߂�B����L�����ꂽ�A���e�i�̋������C���~�����[�g���̐��x�ő��邱�Ƃ��ł���B
�E1�N�Ԃɖ�6cm���n���C�����{�ɋ߂Â��Ă��邪�킩��B
VLBI�ϑ��ǂ̕��ϓI�ȉ^��(���y�n���@)
http://www.spacegeodesy.go.jp/vlbi/image/world.png
--------------------------
�o�x�̗��j�̂܂Ƃ�
�������ǂ��ɂ��邩�́C�ܓx�o�x����m�邱�Ƃ��ł���B�ܓx�͔�r�I�e�Ղɂ킩�邪�C�o�x�����߂邱�Ƃɂ͒�������ł������B�d�M�̔��B�Ő��E�̊e�n�Ƃ̌o�x���r�ł���悤�ɂȂ����B�����̒n�`�}�͓��{���n�n�Ő�������Ă����B�l�H�q���̗��p�Ő����Ȓn���̌`��������C���{���n�n���琢�E���n�n�ֈڍs�����B
=====================
�t�^
�ɁF���c�ՕF�u�n�}���Ȃ��߂āv(���o�@���a�X�N)
https://www.aozora.gr.jp/cards/000042/files/2508_10272.html
����F���a�V�R�ƃ~�}�c�_�C���O����(NHK)2��48�b
https://www2.nhk.or.jp/school/movie/clip.cgi?das_id=D0005401233_00000&p=box
����F�ɔ\���h�̑���(NHK)�@1��55�b
https://www2.nhk.or.jp/school/movie/clip.cgi?das_id=D0005310099_00000
����F���x�]�_�̋L�]�@1��51�b
�@�@https://www.youtube.com/watch?v=RCfIDeioFIs
=============
�Ζʎ��Ƃ���u����Ȏ�u���ւ̉ۑ�
�P�@�]�ˎ���C1800�N����1816�N�܂�17�N�����ē��{�S���𑪗ʂ��āu����{���C�`�n�S�}�v�����������l�͒N���B���O���L���B
2�@�ܓx����ьo�x�Ƃ͉����B���ꂼ��L���B
3 ����⊴�z������Ύ��R�ɏ����Ă��������B
=======================
�ȉ��]��